Semnificatia functiei de transfer

Universitatea Tehnica "Gh. Asachi", Iasi, Facultatea de Electronica si Telecomunicatii

Laboratorul de Semnale, Circuite si Sisteme

Breviar teoretic

Scopul lucrarii:

Caracterizarea circuitului prin ecuatie diferentiala si functie de transfer.

Rezumat teoretic:

Mod de lucru

In afara de functiile incluse in libraria standard Maple, in aceasta lucrare vor fi utilizate cateva functii din libraria aditionala SCSlib.

Pentru calcularea si reprezentarea singularitatilor functiei de transfer:

Ecuatie diferentiala pentru sisteme liniare analogice

Sa consideram ecuatia diferentiala:

> Fy:=(D@@3)(y)(t)-3*(D@@2)(y)(t):Fx:=(D@@2) (e)(t)-e(t):eq:={Fy=Fx}:eq;

Consideram conditii initiale nule pentru iesire. Numarul conditiilor initiale asupra lui si a derivatelor sale este egal cu , ordinul ecuatiei diferentiale.

> initcondy:={y(0)=0,D(y)(0)=0,(D@@2)(y)(0)=0};

In general aceasta ecuatie diferentiala liniara se poate rezolva:

> dsolve(eq union initcondy,y(t));

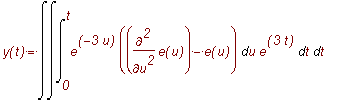
Rezultatul este o expresie pentru in care trebuie sa determinam 2 constante de integrare pe baza conditiilor initiale nule.

Putem considera conditii initiale nule si pentru intrare:

> initcondx:={e(0)=0,D(e)(0)=0}:

Aplicind Transformata Laplace si luind in considerare conditiile initiale nule:

> eqL:=subs(initcondy,laplace(Fy,t,s))=subs(initcondx,laplace(Fx,t,s)):eqL;

> H:=(s)->solve(eqL,Y(s))/E(s):H:=H(s);

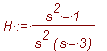
Functia de transfer

Interpretarea functiei de transfer si reprezentarea ei pentru s numar complex:

> H:=s/(s^2+0.1*s+100);

> PZ[numeric](H,s);

> PZ[grafic](H,s);

> plot3d(abs(eval(H,s=sigma+I*omega)),sigma=-2..0,omega=-20..20,axes=normal,title="Reprezentarea in spatiu a modulului f.d.t.");

> plot3d(argument(eval(H,s=sigma+I*omega)),sigma=-0.1..0,omega=-20..20,numpoints = 1000,axes=normal,title="Reprezentarea in spatiu pentru argumentul f.d.t.");

Functia de transfer in regim permanent

> eval(H,s=I*omega);

> plot(abs(eval(H,s=I*omega)),omega=-20..20,axes=normal,title="Reprezentarea modulului f.d.t. pentru regim permanent");

> plot(argument(eval(H,s=I*omega)),omega=-20..20,axes=normal,title="Reprezentarea argumentului f.d.t. pentru regim permanent");

> plots[spacecurve]([omega,Re(eval(H,s=I*omega)),Im(eval(H,s=I*omega)),omega=-20..20],numpoints = 10000,axes=normal,title="Reprezentarea spatiala a F.D.T. pentru regim permanent" );

Probleme

1. Care este semnificatia functiei de transfer? Care este semnificatia functiei de transfer in regim permanent?

2. Sa se refaca etapele de calcul pentru functiile de transfer:

> H := 1/(s+1);

> H:=1/(s+1)/(s^2+10*s+100);